- log3(2x+1) =2.
На оснавании определения логарифма имеем:
2x+1 =32;
2x+1 =9; x =4.
Проверка: x =4; log3(2 *4+1) =log39 =2; 2 =2.
Ответ: x =4. logx+1(2x2+1) =2.
Найдем ОДЗ уравнения: x
(-1; 0)
(0; +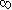
).
По определению логарифма: (x+1)2 =2x2+1;
x2+2x+1 =2x2+1;
x2-2x =0;
x1 =0; x2 =2.
Из двух полученных корней только корень x2 =2 принадлежит ОДЗ, а x1 =0 не принадлежит ОДЗ и, следовательно, является посторонним корнем.
Ответ: x =2.log5x =log5(6=x2).
Найдем ОДЗ уравнения: x >0, x <
.
Применяя метод потенцирования, получим:
x =6-x2;
x2+x-6 =0;
x1 =2; x2 =-3.
Учитывая ОДЗ, отметим, что x2 =-3 - посторонний корень.
Ответ: x =2.lg(x+3) =2lg2-lgx.
Применяя формулы, получаем:
lg(x+3) =lg22-lgx;
lg(x+3) =lg(4/x);
x+3 =4/x;
x2+3x-4 -0;
x1 =1; x2 =-4.
Учитывая проверку, отметим, что x2 =-4 - посторонний корень.
Ответ: x=1.log2(x+14)+log2(x+2) =6.
Применив формулу и учитывая, что 6 =log226, получим:
log2((x+14)(x+2)) =log226;
(x+14)(x+2) =26;
(x+14)(x+2) =64;
x2+16x-36 =0;
x1 =2; x2 =-18.
Учитывая проверку, отметим, что x2 =-18 - посторонний корень.
Ответ: x =2.logx-6(x2-5) =logx-6(2x+19).
x2-5 =2x+19;
x2-2x-24 =0;
x1 =6; x2 =-4.
Учитывая проверку, отметим, что x2 =-4; x1 =6 - посторонний корень.
Ответ: решений нет.log2(9x-1+7) =2+log2(3x-1+1).
Так как 9x-1+7 >0 и 3x-1+1 >0 при x R (по свойству показательной функции), областью определения данного уравнеия является множество всех действительных чисел: x R. Поэтому любой корень уравнения, полученного при потенцировании данного уравнения, посторонним не является.
log2(9x-1+7) =2+log2(3x-1+1);
log2(9x-1+7) =log24+log2(3x-1+1);
log2(9x-1+7) =log2(4 *(3x-1+1));
9x-1+7 =4 *3x-1+4;
32(x-1)-4 *3x-1+3 =0.
Получили показательное уравнение, сводящееся к квадратному.
Положим 3x-1 =y, тогда:
y2-4y+3 =0;
y1 =3; y2 =1.
1)3x-1 =3; x-1 =1; x1 =2;
2)3x-1 =1; x-1 =0; x2 =1;
Ответ: x1 =2; x2 =1.log32x-log3x =2.
Область определения данного уравнения - ОДЗ: x >0. Пусть log3x =у, тогда уравнение примет вид:
y2-y-2 =0.
y1 =2; y2 =-1.
1)log3x =2; x1 =32; x1 =9;
2)log3x =-1; x2 =3-1; x2 =1/3.
Так как x1 >0, x2 >0 то они принадлежат ОДЗ уравнения и являются его корнями.
Ответ: x1 =9; x2 =1/3.log16x+log4x+log2x =7
ОДЗ: x >0. Логарифмы в левой части уравнения приведем к оснаванию 2 по формуле.
log16x =(log2x)/(log216) =(log2x)/4;
log4x =(log2x)/(log24) =(log2x)/2.
((log2x)/4)+((log2x)/2)+log2x =7;
(7/4)log2x =7;
log2x =4; x =16 >0.
Ответ: x=16.log7x+logx7 =2,5.
ОДЗ: x >0, x
1.
logx7 =1/(log7x);
log7x+(1/log7x) =2,5
log72x-2,5 *log7x+1 =0.
Пусть log7x =у, тогда y2-2,5y+1 =0;
y1 =2; y2 =1/2.
1)log7x =2; x2 =49; 2)log7x =1/2; x1 =
;
Ответ: x1 =49; x2 =.
